seaborn
在上一期中,我们详细介绍了matplotlib可视化工具包的使用,毫无疑问,matplotlib是一个用来做可视化非常棒的工具库。然而,大家可能也有所发现,虽然matplotlib画出来的图很精细,但是代码都很长,有些时候会降低我们做事的效率。今天,我们继续推出另外一个更加方便使用的可视化工具包seaborn,它是在matplotlib的基础上做了更高一层的封装,绘图更加简单,样式也更加丰富。
今天,我们仍旧以案例的形式来对seaborn的使用进行说明。
鸢尾花花型尺寸分析
首先在做任何工作之前,先导入相关的工具包。
import numpy as np
import pandas as pd
import seaborn as sns
#为了使图片在notebook中显示出来,添加下边一行
%matplotlib inline
导入鸢尾花数据集。
data = sns.load_dataset("iris")
data.head()
# 萼片长度,萼片宽度,花瓣长度,花瓣宽度,种类
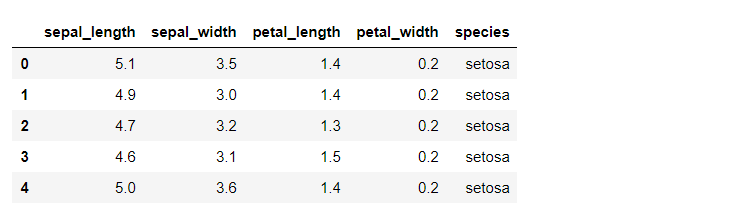
问题一:鸢尾花萼片(sepal)和花瓣(petal)的大小关系
这个问题是分析两个变量之间的关系,用散点图来表示。首先还是要对原始数据做一下处理,分别得到sepal_size和petal_size。
# 首先添加两列表示sepal和petal的大小
data['sepal_size'] = data['sepal_length'] * data['sepal_width']
data['petal_size'] = data['petal_length'] * data['petal_width']
data.head()

#lmplot命令可以用来画散点图及其拟合回归直线
#x和y分别是data中的列名
#size为输出图片的尺寸
sns.lmplot(x = "sepal_size",y = "petal_size",data = data,size = 5)

其中的阴影部分为置信度为95%的置信区间。越往右置信区间越大是由于数据变少,方差变大。总体来看,萼片和花瓣大小呈正相关关系。
问题二:不同种类鸢尾花萼片的分布情况
这个问题是用来查看分类数据的分布情况,这种情况下用seaborn画直方图最为方便了。
sns.boxplot(x = "sepal_size",y = "petal_size",data = data)

可以明显的看出,用seaborn画分类直方图比matplotlib明显方便快捷了很多,只是图形的细节之处,比如箱子的颜色,线的颜色等不太方便调节,这种图比较适合在探索数据分布的过程中使用。
针对这个问题,还可以画小提琴图,这也是一种在探索数据分布过程中使用非常广泛的图形。
sns.violinplot(x = 'species',y = 'sepal_size',data = data)

在这里简单介绍一下小提琴图,小提琴图是箱式图和核密度图的结合。箱式图展示了分位数的位置,中间的白点即是中位数,黑色箱子的上下界是上四分位数和下四分位数。小提琴图外围的曲线是数据的密度分布图,小提琴图则展现了任意位置的密度,通过小提琴图可以知道哪些位置的密度较高。
问题三:鸢尾花萼片和花瓣大小的联合分布情况
在这个问题中,需要绘制联合密度分布图,或者说,我们想要在一个图形中展现出三种鸢尾花的萼片和大小的分布情况。
sns.joinplot(x = "sepal_size",
y = "petal_size",
data = data,
kind = 'kde',
color = 'pink'
)

从这个图中可以看出,图中有三个部分的颜色最深,从这个信息可以看出鸢尾花共有三类,颜色的深浅代表了数据的密集程度。另外,图片上方和右方的曲线分别是横轴和纵轴两个坐标的分布图。
泰坦尼克号海难数据分析
首先还是导入数据。
data = sns.load_dataset('titanic')
data.head()
# 幸存与否,仓位等级,性别,年龄,堂兄弟姐妹数,父母子女数,票价,上船港口缩写,仓位等级,人员分类,是否成年男性,所在甲板,上船港口,是否幸存,是否单独乘船

问题一:不同仓位等级中幸存和遇难乘客的分布
这明显又是一个分类问题,用箱式图或者小提琴图最合适不过了。
sns.violinplot(x = 'class', y = 'survived',data = data)

从这个图中,我们就可以明显的看出,三种仓位等级中幸存和遇难的大致情况(0表示遇难,1表示幸存),很明显,在一等仓中幸存人数多于遇难人数,二等仓中两者比例相当,三等仓中遇难人数最多。这说明幸存与否这个变量是和仓位等级有关的。
问题二:幸存和遇难乘客的票价分布
sns.boxplot(x = 'survive',y = 'fare',data = data)

从这个箱式图中可以发现,箱子已经压得很扁了,这时候可以对纵轴进行对数变换,使箱式图更加美观一些,上一期中介绍过箱式图,有需要的同学请查看上一期“matplotlib可视化案例分析”。
#新增加一列,对“fare”这一列做对数变换
data["lg_fare"] = data["fare"].apply(np.log)
#画箱式图
sns.boxplot(x = 'survive',y = 'lg_fare',data = data)

可以明显看出,经过对数变换后,箱式图美观度增加了很多。在这里做对数变换要舍弃”数据的原始真实值“,把重点放在对比上,因为对数使单调变换的,所以不影响中位数的对比。
对数变换能够使得图形变美观,我有一个比较直观的理解,写出来和大家交流,对数变换之后使得数值被压缩,较大的极端值被缩小,相当于数据的极值被缩小,这样在图上就能够”舒展”开,使得图形变美观。
问题三:幸存和遇难乘客的年龄分布
这同样是一个分类图。把年龄看成连续变量的话,我们同样用箱式图来表示。
sns.boxplot(x = 'survived',y = 'age',data = data)

从这个图中箱子的整体位置,可以粗略得出获救的人的年龄更小一些。
问题四:乘客性别和获救之间的关系
我们都知道在这次灾难中,当时是”妇女和孩子优先“,因此我们想从数据上来看一下性别对最终是否获救的影响。
sns.violinplot(x = 'sex',y = 'survived',data = data)

这个就很明显了,男性中大部分都遇难了,女性中大部分都幸存了。可敬的gentlemen!
问题五:乘客年龄和仓位等级之间的关系
因为之前分析得知一等仓中获救人数最多,三等仓中获救人数最少,我们想看一下是不是年龄越大,仓位等级就越高?于是我们画一下各个仓位中乘客的年龄分布。
#x_jitter是加一个抖动变量,使得点不堆在一起。
sns.lmplot(x = "pclass",y = "age",data = data,x_jitter = 0.1)

从这个图中可以大致看出,确实一等仓乘客的年龄较高一些。但是看起来比较凌乱,可以改用箱式图或者小提琴图来使可视化图形更加形象。
sns.boxplot(x = 'class',y = 'age',data = data)

sns.violinplot(x = 'class',y = 'age',data = data)

从箱式图或者小提琴图上可以明显看出,一等仓乘客的平均年龄最高,二等仓次之,三等仓乘客平均年龄最低。
从上边几个问题的分析中,可以明显的感觉到利用seaborn来画分类关系图是非常方便的,而这也是数据探索过程中非常重要的一个方面,类似的问题还可以提出很多,比如单独乘船与否和幸存的关系, 不同上船港口和乘客幸存与否的关系。 读者可以自行分析。
读者也可以扫码关注我的微信公众号,博客内容会同步进行更新,在微信上交流讨论会更加方便一些。
