注:本文档中的代码和实例是在学习了《机器学习实战》第五章后总结的。
相关jupyter文件及数据集请在我的github上下载。链接如下:
https://github.com/nianshiqiang/machine_learning/tree/master/logistic_regression
logistic regression
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import expit #expit(x) = 1.0 / (1 + exp(-x))
导入数据
#加载数据集
def loadtext():
data = []
label = [] #定义两个空列表用于存储变量数据和标签数据
f = open("logistic regression testSet.txt")
for line in f.readlines():
linearr = line.strip().split()#首先去掉空格,然后分隔字符
data.append([1.0,float(linearr[0]),float(linearr[1])])#注意:需要将字符串类型换为数值型
label.append(int(linearr[2]))
return data,label
定义迭代公式(批处理梯度上升)
def gradascent(variables,classlabels):
datamat = np.mat(variables)
labelmat = np.mat(classlabels).T #将输入的x变量和y变量转换为矩阵
m,n = np.shape(datamat)#得到矩阵的行数和列数
theta = np.ones((n,1))#定义初始theta值
alpha = 0.001
maxcycles = 500
for i in range(maxcycles):
h = expit(datamat * theta)
#print(h)
error = labelmat - h
theta = theta + alpha * datamat.T * error #迭代更新公式
return theta
计算结果
data,label = loadtext()
theta = gradascent(data,label)
theta
#结果
matrix([[ 4.12414349],
[ 0.48007329],
[-0.6168482 ]])
画出决策边界(分界线)
def plotline(theta):
dataarr = np.array(data)#转换为mumpy的array类型
n = np.shape(dataarr)[0]
x0 = []
y0 = []
x1 = []
y1 = []
for i in range(n):
if label[i] == 1:
x0.append(data[i][1])
y0.append(data[i][2]) #将标签值为1的数据存为1组值
else:
x1.append(data[i][1])
y1.append(data[i][2]) #将标签值为0的数据存为另一组值
#开始绘图
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x0,y0,s = 30,c = "red")
ax.scatter(x1,y1,s = 30,c = "green") #绘制散点图
x = np.arange(-3.0,3.0,0.1)
#print(x)
theta = np.array(theta)#重要!!!必须将theta 转换为array类型才能进行运算
y = (-(theta[0])-theta[1] * x) / theta[2]
ax.plot(x,y)
plt.xlabel("X1")
plt.ylabel("X2")
plt.show()
plotline(theta)
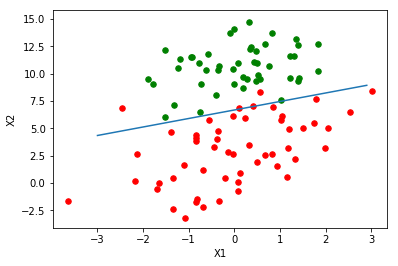
随机梯度上升
def stocgradascent(variables,classlabels):
datamat = np.mat(variables)
labelmat = np.mat(classlabels).T #将输入的x变量和y变量转换为矩阵
m,n = np.shape(datamat)#得到矩阵的行数和列数
theta = np.ones((n,1))#定义初始theta值
alpha = 0.01
#maxcycles = 500
for i in range(m):#迭代次数为训练集的个数,重要!!
h = expit(datamat[i] * theta)#计算每一个训练样本的h值
error = labelmat[i] - h
theta = theta + alpha * datamat[i].T * error #迭代更新公式
return theta
data,label = loadtext()# 继续使用testSet.txt的数据
stoc_theta = stocgradascent(data,label)
stoc_theta
#结果
matrix([[ 1.01702007],
[ 0.85914348],
[-0.36579921]])
plotline(stoc_theta)
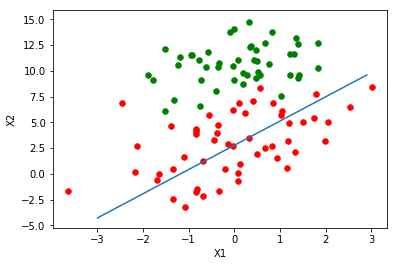
实例:从疝气病症预测病马的死亡率
- 数据来源:http://archive.ics.uci.edu/ml/datasets/Horse+Colic
- 有两个文件,分别为训练集horseColicTraining.txt和测试集horseColicTest.txt
- 数据集中有21个特征,1个label(0 or 1)
def classifyfunc(x): #定义一个分类函数
prob = expit(x) #计算logistic函数
if prob > 0.5:
return 1.0
else:
return 0
def colictest(): #定义一个分类器
ftrain = open("horseColicTraining.txt") #打开训练集
ftest = open("horseColicTest.txt") #打开测试集
for line in ftrain.readlines():
currline = line.strip().split()
trainning_set = [] #存放特征值的list
trainning_label= [] #存放label的list
for i in range(21): #因为有21个特征
trainning_set.append(float(currline[i]))
trainning_label.append(float(currline[21]))#前21个为特征向量,最后一列为label值
trainning_theta = stocgradascent(trainning_set,trainning_label)
#计算分类准确度
error_count = 0
num_test = 0
for line in ftest.readlines():
num_test+=1
currline = line.strip().split()
linearr = []
for i in range(21): #因为有21个特征
linearr.append(float(currline[i]))
h = np.mat(linearr) * trainning_theta #将特征值和对应的theta值相乘后相加
if classifyfunc(h) != int(currline[21]): #预测值和真实值的比较
error_count += 1
error_rate = error_count / num_test #计算分类准确度
print("the error_rate is %f" %error_rate)
return error_rate
colictest()
the error_rate is 0.298507
0.29850746268656714